Ces recherches constituent une thématique novatrice démarrée en 2004 ayant pour objectif de prospecter sur le traitement que l’on peut faire d’images de spray de façon à extraire un maximum d’information. Il s’agit donc d’un post-traitement de données expérimentales, mais ouvre des perspectives intéressantes d’analyse et de représentation des phases dispersées. D’ailleurs ces techniques de représentation fractales sont de plus en plus fréquentes dans la littérature des sprays et des phases particulaires. Deux étudiants de master de l’UPMC (V. Freire 2005 et S. Roudnitsky 2004) ont participé à ces activités.

 

Dimensions de recouvrement

 

Dimension de Hausdorff-Besicovitch

Une première approche pour mesurer la dimension d’un objet E consiste à suivre la méthode habituelle de pavage de l’objet par des pavés (appartenant à l’espace dans lequel l’objet est plongé) de mesure où d(E) est la dimension de l’objet. Mais lorsque d(E) est à priori inconnue, une solution consiste à faire des essais en prenant des unités de mesure avec un exposant α indéterminé.

L’objet étant de forme quelconque, en général, il n’est pas possible de le recouvrir avec des pavés identiques de côté η. Cependant il est possible de réaliser le recouvrement de l’objet E avec des boules V_i dont le diamètre (diam V_i) est inférieur ou égale à η. Ceci offre plus de souplesse mais impose de prendre la limite inférieure de la somme des mesures élémentaires.

 

La α-mesure de recouvrement est ainsi définie (d’après Hausdorff (1919) et Besicovitch (1935) :

et la dimension de Hausdorff (ou Hausdorff-Besicovitch), dim E est alors définie par :

La dimension de Hausdorff est la valeur de α pour laquelle la mesure fait un saut de zéro à l’infini. Pour la valeur , cette mesure peut être quelconque entre zéro et l’infini.

 

Dimension de Bouligand-Minkowski

Il est également possible de définir une dimension dite de Bouligand-Minkowski, (Bouligand, 1929, Minkowski, 1901), que l’on note Δ(E). Il existe plusieurs méthodes afin de calculer Δ(E) :

 

▪ La méthode des boîtes :

Soit N(η) le nombre de pavés de côté η recouvrant E :      

 

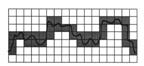
Figure 10: Mesure de la dimension d’une courbe par la méthode des boîtes

 

La méthode des boîtes est couramment utilisée, en particulier pour les structures auto-affines.

 

▪ La méthode des boules disjointes :

Soit N(η) le nombre maximum de boules disjointes de rayon η centrées sur l’ensemble E, alors :

 

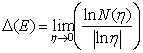
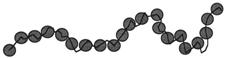
Figure 11: Mesures de la dimension d’une courbe par la méthode des boules disjointes

 

Application aux sprays

 

L’étude est réalisée à partir d'un nombre considérable de clichés pris par P.I.V. (Particle Imaging Velocimetry) des sprays. Une nappe lumineuse obtenue à partir d’un laser éclaire une section médiane du jet pendant un temps très court à un instant précis après le début de l’injection.

Les séries d’images ont été prises sous différentes pressions, pour différentes températures et à différents instants ΔT : 350, 500, 750, 1000, 1500 …après le début de l’injection. L'injecteur étudié est du type "outward opening" , la soupape de sortie étant d'un diamètre de 3mm et le système d'injection du type "à impulsion" ou coup de bélier sous un pression de 40bar, le liquide étant du gasoil commercial (c.f. Stan et al. ^[STA/05]).

Dans un premier temps, on considère chaque ligne de pixels de l'image comme un ensemble de Cantor, dont on détermine une dimension fractale uniquement fonction de l’ordonnée (z) correspondant au numéro de la ligne considérée  et définie par :

N représentant le nombre de segments occupés par des gouttes, l’échelle ou taille des segments et la dimension fractale. Cette dernière est un nombre compris entre 0 et 1.

Pour chaque ligne, nous obtenons ainsi une dimension fractale unique représentée par la pente de la droite d’équation :

Mais en observant les courbes représentant le nombre de gouttes N en fonction de l’échelle , on remarque que pour les zones où le spray est développé (loin de l'injecteur) la régression linéaire ne représente pas correctement la relation N – l.

L’ensemble des points est alors ajusté à une régression polynomiale d’ordre 2 :

        

La régression pour chaque ligne a été obtenue en moyennant les 50 relations N-l déduites de chaque cliché à un temps fixé.

 

Un facteur de qualité basé sur les moindres carrés montre que la régression retenue est bien adaptée .

Figure 14: Allures des régressions représentant le nombre de boîtes en fonction de l’échelle  à 500 μs après l’injection

 

Nous noterons que la régression d’ordre 2 fournit des coefficients a négatifs pour la plupart des lignes, exceptées pour certaines correspondant à des endroits particuliers du spray (début et fin de la zone à forte densité de gouttelettes).

La dimension fractale est alors obtenue par la pente de la courbe :

La dimension fractale dépend ainsi de l’ordonnée z mais surtout de l’échelle de résolution . La fractalité est considérée localement en échelle.

La Figure 15 montre l’évolution de cette dimension en fonction de la distance au nez de l’injecteur pour trois différentes échelles à un instant donné. Entre z=80 (atomisation) et z=320 (extrémité du spray) la dimension passe, quelque soit l’échelle par un maximum correspondant à la zone de développement transversal maximal du spray. Cette évolution traduit en premier lieu la capacité du spray à couvrir le plan d’observation et son maximum correspond bien à une zone de dispersion maximale des gouttes sans perte apparente de densité.

Figure 15: Dimension fractale en fonction de  l’échelle et de l’ordonnée

La Figure 16 montre les mêmes évolutions pour différents moments de l’injection. Il est intéressant de noter comment la morphologie du spray semble bien liée à l’évolution de la dimension, et comment cette relation devient plus complexe pour les petites échelles.

Figure 16: Dimension fractale en fonction de  l’échelle, de l’ordonnée et du temps

 

Ces exemples montrent une dépendance forte des variations de la dimension avec différentes configurations du spray. Idéalement, ces variations doivent être reliées quantitativement à différents processus physiques affectant l'évolution du spray. Comme le montrent les évolutions des figures suivantes, les paramètres physiques majeurs comme la pression et la température influencent fortement la dimension telle qu'elle a été étudiée.

 

▪P=1 bar, T=25°C,  z=220            : ▪P=1 bar, T=200°C, z=180 :

▪P=5 bars, T=25°C, z=190 :▪P=10 bars, T=25°C, z=136

Figure 17: Dimension fractale en fonction de  l’échelle, du temps, de la pression et de la température

 

Ces courbes permettent d’observer que petites et grandes échelles se détachent d’autant plus que la pression augmente et la température diminue. En effet, à pression et température atmosphériques, petites et grandes échelles sont pratiquement confondues.

 

▪T=25°C,  , z=287 et P=1,5,10 bars :       ▪P=1 bar,  , z=220 et T=25,200°C :

Figure 18: Dimension fractale en fonction de  l’échelle, de la pression et de la température

 

 

Ces courbes montrent que la dimension fractale est fonction décroissante de la pression et de la température quelque soit l’échelle.

 

La théorie des peaux entropiques

 

Afin de mieux comprendre la dépendance en échelle et en temps de la dimension fractale il nous a semblé intéressant d'introduire des équations d'échelle de façon à tenir compte dans les sprays étudiés de l'écart par rapport au cas auto similaire. Une forme simple d'introduire une équation d'échelle est développée par D. Queiros-Conde ^{[QUE/01] et [QUE/03]}, sous la forme d'entropie d'échelle.

Queiros-Conde^[QUE/03] quantifie la variation de la dimension fractale en fonction de l’échelle à l’aide d’une géométrie entropique afin de décrire pleinement la turbulence.

On a :

 désigne l’échelle et vérifie :

 désigne la dimension fractale et vérifie :

Soit , le nombre de boules de diamètre nécessaires afin de couvrir un champ de diamètre .

Soit , le volume occupé par à l’échelle obtenu en couvrant :

 avec d représentant la dimension de l’espace.

Soit , le volume total occupé par à l’échelle  :

 avec

Le rapport définit la fraction volumique de dans , alors que l’inverse de ce rapport représente le nombre de nécessaires pour remplir .

Afin de quantifier le désordre de par rapport à , Queiros-Conde^[QUE/03] introduit une échelle d’entropie définie par :

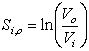
Remarque : Malgré les apparences, cette définition ne traduit pas une approche de physique statistique du problème. Elle est équivalente néanmoins à la notion de e-entropie introduite par Kolmogorov ^[KOL/56].

 

Afin de décrire le saut d’entropie entre deux éléments consécutifs et tels que et , on définit un flux d’entropie qui quantifie l’évolution d’entropie au travers de l’échelle spatiale:

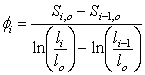
Ce flux est négatif et de valeur opposée à celui de la codimension de définie par :

En posant :                                            

La relation s’écrit :                                                

La valeur du flux varie selon la densité de flux d’entropie, notée est définie par :

 

En considérant le cas où la densité de flux est indépendante de l’échelle, c’est-à-dire :, les deux relations précédentes permettent d’écrire :

 , ce qui implique par intégration : 

Notons que le cas auto-similaire (fractal) correspond à une valeur nulle de la densité de flux.

 

Or par définition, 

L’intégration entraîne alors :

En égalisant les deux expressions de obtenues par intégration, nous obtenons :

 

Le coefficient peut alors être identifié à l’aide des courbes expérimentales obtenues précédemment à l’aide de la régression d’ordre 2 :

Par identification :

 

Par ailleurs, ce même coefficient représente la pente des droites donnant la dimension fractale en fonction de l’échelle :

Puisque lorsque , et lorsque , , alors le coefficient est défini par :

Remarque : Il est également possible de retrouver expérimentalement la valeur de ce coefficient  à l’aide d’une régression d’ordre 1: .

Par identification :

 

Expérimentalement, on constate que ce coefficient varie également en fonction du temps. Par exemple, en considérant les clichés pris à 500,750 et à 1000  après le début de l’injection, sous une pression de 5 bars, à température atmosphérique comme sur la figure suivante :

Figure 19: Coefficient β en fonction de l’ordonnée et du temps, pression et températures atmosphériques

 

Les figures suivantes montrent l’évolution du coefficient pour trois niveaux de pression (à température ambiante) et deux niveaux de température (à pression ambiante) dans l’enceinte, en fonction de l’abscisse (distance au nez de l’injecteur).

Figure 20 : Coefficient β en fonction de l’ordonnée pour trois niveaux  de pression,1, 5 et 10 bar

Figure 21: Coefficient β en fonction de l’ordonnée pour deux niveaux de température, 25°C et 200°C

L’observation de ces courbes montre que les zones où est négatif sont d'autant plus étendues que la pression est faible et la température élevée, c’est-à-dire lorsque l'évaporation des gouttes augmente.  Aussi, il serait intéressant de vérifier cette relation empirique et établir des relations formelles entre cette formulation et des processus physiques dans le spray.

 

Cette étude permet d'entrevoir une méthode originale de traitement des images de spray. Une étape en cours passe par l'étude des dimensions fractales et de leur diffusion non seulement en temps et espace mais aussi en niveau de gris, c'est à dire en population de gouttes. Si elle aboutit, elle rendrait compte de l'évolution de la masse liquide de façon indirecte. L'intérêt d'une telle méthode réside dans le fait qu'elle semble pouvoir renseigner sur un certain nombre de tendances qu'il est difficile d'extraire de simples images de diffusion des gouttes. Elle permettrait d'extraire de l'information importante en termes de qualité de mélange (taux d'évaporation et de diffusion) ou du moins les tendances relatives sans passer par des techniques plus onéreuses de mesure.

Elle permettrait au moins dans un premier temps, d'aborder la dilution relative du spray et caractériser ainsi différentes géométries d'injecteur ou systèmes d'injection en regard de ce paramètre crucial qu'est la dilution, car les dimensions de recouvrement mesurent justement la capacité d'un objet géométrique (ici le spray) à couvrir l'espace qui le contient.

Dans ce contexte, elle peut s'appliquer à caractériser la façon dont le spray interagit avec le milieux gazeux environnant.